LE CARRÉ INVERSE S’APPLIQUE EN SON COMME EN LUMIÈRE
Dans l’environnement, le comportement du son comme celui de la lumière dépendent de lois physiques, qui s’appliquent aussi à bien d’autres grandeurs. Ainsi, la loi du carré inverse, que l’on rencontre fréquemment dans nos univers sous le nom de « inverse square law », traduit-elle le profil de l’atténuation de l’intensité énergétique de façon inversement proportionnelle au carré de la distance avec sa source.
En introduction, situons les notions de proportions entre grandeurs. On parle de situation « directement proportionnelle » lorsque les deux valeurs liées évoluent, à la hausse ou à la baisse, dans le même sens. Posons y ∝ x (∝ signifie « est proportionnel à »). Quand x augmente, y fait de même. Quand x diminue, y aussi.
Dans une situation « inversement proportionnelle », les deux valeurs liées évoluent… inversement. Si y ∝ 1/x, lorsque x augmente, y diminue. Si x diminue, y augmente.
Considérons un exemple concret. Un tourbus part du Zénith de Rouen pour rejoindre celui de Montpellier, soit 850 km dans la joie et la bonne humeur. Si le chauffeur roule à une vitesse moyenne de 85 km/h, dix heures seront nécessaires pour faire le trajet. S’il a un imprévu en route, qui baisse sa moyenne à 60 km/h, plus de quatorze heures seront nécessaires pour atteindre Montpellier. Le spectacle du jour sera compromis, mais là n’est pas la question. Vitesse moyenne (Vm) et durée (T) du trajet sont liées suivant la loi de la proportion inverse par la formule T = 850 / Vm. Si la vitesse moyenne augmente, le temps du trajet diminue, et vice versa.
La proportion en carré inverse répond aux mêmes principes que la proportion inverse, à cela près que la grandeur en dénominateur est placée au carré, ce qui s’exprime y ∝ 1/x².
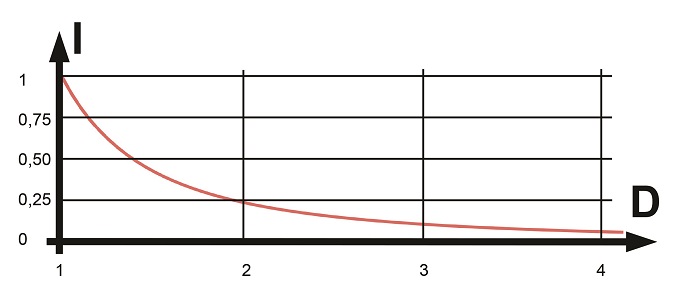
Un extrait du tracé de la courbe y = 1/x2 représentative de la loi en carré inverse. Pour x = 1, y = 1. Quand x double, y est divisé par 22=4. Et pour un x quadruple, la valeur de y est diminuée d’un facteur 42=16
UN DESSIN VAUT MILLE ÉQUATIONS
Pour comprendre l’application concrète dans nos univers de cette loi de proportion en carré inverse, inutile d’aller plus loin pour l’instant dans les équations mathématiques. Un simple dessin géométrique exprime parfaitement l’effet (fig. 1).
Imaginons une source d’énergie E ponctuelle omnidirectionnelle, dans un milieu « parfait », c’est-à-dire sans obstacles, ni atmosphériques (fumée, humidité…) ni physiques (murs, cloisons, plafond…).Que ce soit du son ou de la lumière, la quantité d’énergie émise par la source E va se disperser sous la forme d’une sphère dont le rayon va augmenter au fur et à mesure que l’onde énergétique va s’éloigner de la source.
Considérons la quantité d’énergie se déployant sur une portion de la sphère correspondant à un angle solide donné, à une distance de la source que nous appellerons le rayon initial mesurant la longueur d1. En doublant ce rayon, donc en se retrouvant à 2.d1, que sera devenue la surface ?
La surface d’une sphère s’exprime par s = 4.π.r². Le rayon r étant au carré, chaque doublement de longueur va donc induire une multiplication de la surface par 2² = 4.
Or, la portion de l’énergie de notre source E, que l’on trouvait répartie sur l’ensemble de la surface S1, a fait son chemin. A la distance 2.d1, elle se retrouve, géométriquement dispersée sur une surface quatre fois plus importante que S1. Par unité de surface, l’énergie disponible sur la zone sera donc quatre fois inférieure à celle présente, toujours par unité de surface, sur la zone S1. C’est le principe de la loi du carré inverse.

APPLICATION À LA LUMIÈRE
En théorisant cette loi du carré inverse, Isaac Newton a montré qu’elle s’applique aux intensités dans de multiples domaines, électricité, magnétisme, radiation et lumière.
Rappelons que ces principes s’entendent dans un environnement « idéal », c’est-à-dire sans obstacle, qu’ils soient physiques ou atmosphériques. Un brouillard dans la salle, par exemple, va diffuser les rayons lumineux et complètement modifier le comportement de la lumière.
Dans un environnement idéal, donc, l’intensité d’un rayonnement lumineux va être divisée par 4 à chaque doublement de la distance parcourue par les rayons.
La figure 2 est une représentation en deux dimensions du comportement d’un faisceau lumineux avec la distance. Cette vue nous permet d’exprimer clairement l’atténuation de l’éclairement (en lux). Le luminaire délivre en sortie d’optique un flux lumineux, soit une quantité totale de lumière donnée (en lumen). Dans un environnement « parfait », ce flux va rester identique quelle que soit la distance. Mais comme la section du faisceau augmente proportionnellement au carré de la distance, le flux global se dilue sur une surface de plus en plus grande.
A une distance de 20 mètres, l’éclairement ponctuel ne sera plus que le seizième de ce qu’il était à cinq mètres. Un point à sérieusement prendre en compte donc dans un design lumière.
APPLICATION AU SON
Considérons une source sonore ponctuelle, déployant donc son énergie suivant une onde sphérique autour de son point d’origine. Nous supposerons des conditions acoustiques idéales, c’est-à-dire et dans une atmosphère neutre et en champ libre. Tout obstacle induirait en effet des réflexions et par voie de conséquence des interférences acoustiques destructives qui conduiront à une modification du comportement.
Comme pour notre énergie lumineuse, il y a un transfert de l’énergie sonore de la source, suivant une sphère de rayon croissant. L’énergie initiale totale se répartit uniformément sur l’ensemble de la surface de la sphère. Quand son rayon double, nous avons vu que sa surface quadruple, l’intensité sonore par unité de surface (exprimée en W/m2) se divise donc par quatre.
Il y a donc bien un respect de la loi du carré inverse pour l’atténuation de l’intensité sonore avec la distance.
Pour autant, nous sommes bien moins familiers des valeurs d’intensités acoustiques, exprimées en W/m2, que de celles en dB, qui désignent les niveaux d’intensité sonore (L).Les deux notions sont liées par l’équation L = 10 log I/Io. I désignant l’intensité sonore considérée et Io celle de référence.
Pour exprimer un niveau d’intensité sonore « absolu », on se base sur une valeur Io de référence correspondant au seuil d’audition, le son le plus faible que nos oreilles sont capables de percevoir. Et son intensité sonore s’élève à 10-12 W/m2.Pour revenir à notre loi du carré inverse, nous allons chercher à trouver combien de dB séparent les niveaux d’intensité sonore à chaque doublement de distance, donc entre une intensité sonore de Io et celle de I = I/4 que l’on trouve en doublant la distance.
L = 10 log I/Io = 10 log I/4I = 10 log ¼ = – 6,02 dB







